차원 축소(Dimensionality Reduction)
01 Sep 2020 | Machine-Learning
해당 게시물은 고려대학교 강필성 교수님의 강의를 바탕으로 작성한 것입니다.
Dimensionality Reduction
차원 축소(Dimensionality reduction)란 데이터가 가지고 있는 특성의 개수를 줄여나가면서 모델의 성능을 유지하는 방법입니다. 차원 축소를 하는 이유는 무엇일까요? 데이터 과학에서는 이른바 차원의 저주(Curse of dimensionality)라는 용어를 사용합니다. 차원의 저주가 의미하는 바는 다음과 같습니다.
“특성의 개수가 선형적으로 늘어날 때 동일한 설명력을 가지기 위해 필요한 인스턴스의 수는 지수적으로 증가한다. 즉 동일한 개수의 인스턴스를 가지는 데이터셋의 차원이 늘어날수록 설명력이 떨어지게 된다.”
아래 예시는 차원의 저주를 단적으로 보여주는 이미지입니다.
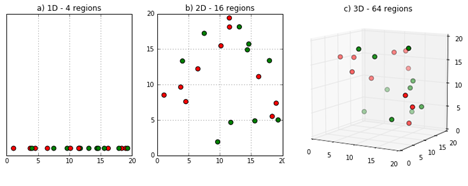
이미지 출처 : deepai.org
위 그림에는 총 20개의 인스턴스로 이루어진 데이터셋이 있습니다. 왼쪽부터 데이터셋이 각각 1차원, 2차원, 3차원 공간 속에 있을 때 인스턴스가 어떻게 위치하는 지를 나타내고 있습니다. 1차원(직선) 공간에 위치할 때에는 인스턴스들이 굉장히 조밀하게 배치되어 있슨 것을 알 수 있습니다. 이 중 몇몇 인스턴스는 2차원 공간에서 꽤 멀어지게 됩니다. 3차원 공간에서는 어떻게 될까요? 비록 위 그림에서 직관적으로 느껴지지는 않지만 아마 2차원에서 보다도 더욱 멀어질 것입니다. 이렇게 데이터의 차원이 커지면 인스턴스는 멀리 떨어져 있게 되고 데이터가 희소(Sparse)해지면서 설명력이 떨어지는 문제가 발생합니다.
하지만 데이터에게 중요한 본질적인 차원 수는 겉으로 드러나는 차원 수보다 더 적을 확률이 많습니다. MNIST 손글씨 데이터도 겉으로는 $768(=24 \times 24)$ 차원으로 구성된 데이터이지만 중간중간 데이터를 제거 하더라도 구분하는 데에는 큰 지장이 없습니다. 아래는 ISOMAP으로 MNIST 손글씨 데이터를 시각화하여 나타낸 것입니다. 이렇게 2차원으로 급격히 차원수를 줄이더라도 어느정도 분류되는 것을 볼 수 있습니다.

이미지 출처 : blog.paperspace.com
모든 특성이 독립이라는 가정이 있다면 특성의 개수가 늘어날수록 예측 모형의 성능은 증가해야 합니다. 하지만 현실적으로 이런 가정은 불가능 합니다. 게다가 고차원의 데이터에서는 변수에 포함될 노이즈의 합도 늘어나기 때문에 예측 모형의 성능이 점점 떨어지게 되는 문제도 발생합니다. 또한 모델을 생성할 때 행렬 연산을 해야하는데 차원이 커질수록 학습 시간이 늘어난다는 단점도 있습니다.
차원의 저주를 풀기 위한 방법 중 가장 간단한 것은 도메인 지식(Domain knowledge)을 활용하는 것입니다. 해당 분야에 대해 잘 알고 있는 사람이 데이터셋에서 중요도가 떨어지는 특성을 삭제하게 됩니다. 두 번째 방법은 만들고자 하는 모델의 목적 함수(Objective function)에 정규화(Regularization)를 사용하는 것입니다. 선형 회귀에 정규화를 사용하는 대표적인 방법으로 릿지(Ridge)와 라쏘(Lasso) 등이 있습니다. 마지막으로 기술적으로 차원의 수를 줄이는 방법을 사용하는 방법이 있습니다.
이런 차원 축소 방법을 사용하여 변수 간 상관관계를 줄일 수 있으며 중요한 정보를 유지하면서도 불필요한 정보를 줄일 수 있습니다. 게다가 데이터 후처리(Post-processing)을 간단히 할 수 있고 시각화(Visualization)도 가능하다는 장점이 있습니다.
Type of Dimensionality Reduction
Supervised vs Unsupervised
차원 축소는 크게 지도 학습(Supervised learning)을 기반으로 하는 방법과 비지도 학습(Unsupervised learning)을 기반으로 하는 방법으로 나눌 수 있습니다. 비지도 학습 기반에는 없었던 피드백 루프(Feedback loop)가 지도 학습 기반의 차원 축소에는 등장한다는 점에서 차이점을 가집니다.
지도 학습 기반의 차원축소에서는 이 피드백 루프를 통해서 가장 적합한 특성 조합을 찾을 때까지 알고리즘을 통해 반복 학습합니다. 아래는 지도 학습 기반의 차원 축소를 그림으로 나타낸 것입니다.

이미지 출처 : github.com/pilsung-kang/Business-Analytics-IME654
반대로 비지도 학습 기반의 차원 축소에는 피드백 루프가 없습니다. 비지도 학습 기반의 차원 축소를 사용하면 반복없이 하나의 메커니즘을 통해 특성의 수를 줄일 수 있습니다.
지도 학습의 기반의 차원축소 방식 중 유전 알고리즘 방식은 랜덤으로 난수를 선택하기 때문에 최종적으로 선택된 특성이 매번 달라질 수 있습니다. 하지만 비지도 학습 기반 방식은 동일한 데이터에 동일한 알고리즘을 적용한다면 항상 같은 결과를 보여준다는 특징을 가지고 있습니다. 아래는 비지도 학습 기반의 차원 축소를 그림으로 나타낸 것입니다.

이미지 출처 : github.com/pilsung-kang/Business-Analytics-IME654
Feature Selection vs Feature Extraction
차원 축소를 실행한 뒤에 나오는 특성의 결과가 어떤 지에 따라서도 차원 축소를 2가지로 나눌 수 있습니다. 첫 번째는 특성 선택(Feature selection)입니다. 특성 선택 방법에서는 전체 특성 중에서 유의미한 것으로 판단되는 특성의 부분 집합을 선택합니다. 특성 선택은 선택과 학습이 일어나는 시점에 따라 다시 두 가지 방법으로 나눌 수 있습니다. 필터(Filter)는 특성 선택과 모델의 학습이 독립적인 경우이며 래퍼(Wrapper)에서는 모델은 최적화하는 과정에서 동시에 변수 선택이 이루어집니다.
두 번째 차원 축소 방법인 특성 추출(Feature extraction)은 기존 특성의 조합을 통해서 새로운 특성을 만들어냅니다. 이 때 만들어진 새로운 특성은 데이터를 더욱 잘 나타내는 특성이 되며, 추출되어 나온 특성의 개수는 당연히 원래 특성의 개수보다 적습니다.
아래는 특성 선택과 특성 추출을 비교하여 나타낸 이미지입니다. 기존 데이터의 특성 $X_m (m = 1,\cdots,n)$ 에 대하여 특성 선택에서는 특성의 개수를 $n$보다 줄이는 방법을, 특성 추출에서는 기존 특성을 조합하여 새로운 특성 집합인 $Z$를 만드는 것을 볼 수 있습니다.

이미지 출처 : github.com/pilsung-kang/Business-Analytics-IME654
아래는 차원 축소를 특성 선택과 특성 추출로 분류한 뒤 방법에 따라 한 번더 분류한 그림입니다.

이미지 출처 : github.com/pilsung-kang/Business-Analytics-IME654
우선 특성 선택 중 필터 방법은 알고리즘을 사용하지 않는 방법이며 정보 획득량(Information gain, IG)이나 오즈비(Odds ratio) 등의 수치를 사용하여 특성을 평가합니다. 래퍼 방법에서는 알고리즘을 사용합니다. 전진 선택법(Forward selection), 후진 제거법(Backward elimination), 유전 알고리즘(Genetic algorithm) 등이 이에 속합니다.
특성 추출은 어떤 것에 중점을 두느냐에 따라 세 가지로 나누어 볼 수 있습니다. 첫 번째는 분산을 최대한으로 보존하는 방법이며 주성분분석(Principle component analysis)이 이 방법에 속합니다. 두 번째는 인스턴스간의 거리 정보를 최대화하는 것으로 다차원 스케일링(Multidimensional scaling)이 있습니다. 마지막으로 잠재된 비선형 구조를 찾는 방법이 있습니다. 지역적 선형 임베딩(Locally linear embedding, LLE), ISOMAP, t-SNE 등이 모두 이에 속합니다.
해당 게시물은 고려대학교 강필성 교수님의 강의를 바탕으로 작성한 것입니다.
Dimensionality Reduction
차원 축소(Dimensionality reduction)란 데이터가 가지고 있는 특성의 개수를 줄여나가면서 모델의 성능을 유지하는 방법입니다. 차원 축소를 하는 이유는 무엇일까요? 데이터 과학에서는 이른바 차원의 저주(Curse of dimensionality)라는 용어를 사용합니다. 차원의 저주가 의미하는 바는 다음과 같습니다.
“특성의 개수가 선형적으로 늘어날 때 동일한 설명력을 가지기 위해 필요한 인스턴스의 수는 지수적으로 증가한다. 즉 동일한 개수의 인스턴스를 가지는 데이터셋의 차원이 늘어날수록 설명력이 떨어지게 된다.”
아래 예시는 차원의 저주를 단적으로 보여주는 이미지입니다.

이미지 출처 : deepai.org
위 그림에는 총 20개의 인스턴스로 이루어진 데이터셋이 있습니다. 왼쪽부터 데이터셋이 각각 1차원, 2차원, 3차원 공간 속에 있을 때 인스턴스가 어떻게 위치하는 지를 나타내고 있습니다. 1차원(직선) 공간에 위치할 때에는 인스턴스들이 굉장히 조밀하게 배치되어 있슨 것을 알 수 있습니다. 이 중 몇몇 인스턴스는 2차원 공간에서 꽤 멀어지게 됩니다. 3차원 공간에서는 어떻게 될까요? 비록 위 그림에서 직관적으로 느껴지지는 않지만 아마 2차원에서 보다도 더욱 멀어질 것입니다. 이렇게 데이터의 차원이 커지면 인스턴스는 멀리 떨어져 있게 되고 데이터가 희소(Sparse)해지면서 설명력이 떨어지는 문제가 발생합니다.
하지만 데이터에게 중요한 본질적인 차원 수는 겉으로 드러나는 차원 수보다 더 적을 확률이 많습니다. MNIST 손글씨 데이터도 겉으로는 $768(=24 \times 24)$ 차원으로 구성된 데이터이지만 중간중간 데이터를 제거 하더라도 구분하는 데에는 큰 지장이 없습니다. 아래는 ISOMAP으로 MNIST 손글씨 데이터를 시각화하여 나타낸 것입니다. 이렇게 2차원으로 급격히 차원수를 줄이더라도 어느정도 분류되는 것을 볼 수 있습니다.

이미지 출처 : blog.paperspace.com
모든 특성이 독립이라는 가정이 있다면 특성의 개수가 늘어날수록 예측 모형의 성능은 증가해야 합니다. 하지만 현실적으로 이런 가정은 불가능 합니다. 게다가 고차원의 데이터에서는 변수에 포함될 노이즈의 합도 늘어나기 때문에 예측 모형의 성능이 점점 떨어지게 되는 문제도 발생합니다. 또한 모델을 생성할 때 행렬 연산을 해야하는데 차원이 커질수록 학습 시간이 늘어난다는 단점도 있습니다.
차원의 저주를 풀기 위한 방법 중 가장 간단한 것은 도메인 지식(Domain knowledge)을 활용하는 것입니다. 해당 분야에 대해 잘 알고 있는 사람이 데이터셋에서 중요도가 떨어지는 특성을 삭제하게 됩니다. 두 번째 방법은 만들고자 하는 모델의 목적 함수(Objective function)에 정규화(Regularization)를 사용하는 것입니다. 선형 회귀에 정규화를 사용하는 대표적인 방법으로 릿지(Ridge)와 라쏘(Lasso) 등이 있습니다. 마지막으로 기술적으로 차원의 수를 줄이는 방법을 사용하는 방법이 있습니다.
이런 차원 축소 방법을 사용하여 변수 간 상관관계를 줄일 수 있으며 중요한 정보를 유지하면서도 불필요한 정보를 줄일 수 있습니다. 게다가 데이터 후처리(Post-processing)을 간단히 할 수 있고 시각화(Visualization)도 가능하다는 장점이 있습니다.
Type of Dimensionality Reduction
Supervised vs Unsupervised
차원 축소는 크게 지도 학습(Supervised learning)을 기반으로 하는 방법과 비지도 학습(Unsupervised learning)을 기반으로 하는 방법으로 나눌 수 있습니다. 비지도 학습 기반에는 없었던 피드백 루프(Feedback loop)가 지도 학습 기반의 차원 축소에는 등장한다는 점에서 차이점을 가집니다.
지도 학습 기반의 차원축소에서는 이 피드백 루프를 통해서 가장 적합한 특성 조합을 찾을 때까지 알고리즘을 통해 반복 학습합니다. 아래는 지도 학습 기반의 차원 축소를 그림으로 나타낸 것입니다.

이미지 출처 : github.com/pilsung-kang/Business-Analytics-IME654
반대로 비지도 학습 기반의 차원 축소에는 피드백 루프가 없습니다. 비지도 학습 기반의 차원 축소를 사용하면 반복없이 하나의 메커니즘을 통해 특성의 수를 줄일 수 있습니다.
지도 학습의 기반의 차원축소 방식 중 유전 알고리즘 방식은 랜덤으로 난수를 선택하기 때문에 최종적으로 선택된 특성이 매번 달라질 수 있습니다. 하지만 비지도 학습 기반 방식은 동일한 데이터에 동일한 알고리즘을 적용한다면 항상 같은 결과를 보여준다는 특징을 가지고 있습니다. 아래는 비지도 학습 기반의 차원 축소를 그림으로 나타낸 것입니다.

이미지 출처 : github.com/pilsung-kang/Business-Analytics-IME654
Feature Selection vs Feature Extraction
차원 축소를 실행한 뒤에 나오는 특성의 결과가 어떤 지에 따라서도 차원 축소를 2가지로 나눌 수 있습니다. 첫 번째는 특성 선택(Feature selection)입니다. 특성 선택 방법에서는 전체 특성 중에서 유의미한 것으로 판단되는 특성의 부분 집합을 선택합니다. 특성 선택은 선택과 학습이 일어나는 시점에 따라 다시 두 가지 방법으로 나눌 수 있습니다. 필터(Filter)는 특성 선택과 모델의 학습이 독립적인 경우이며 래퍼(Wrapper)에서는 모델은 최적화하는 과정에서 동시에 변수 선택이 이루어집니다.
두 번째 차원 축소 방법인 특성 추출(Feature extraction)은 기존 특성의 조합을 통해서 새로운 특성을 만들어냅니다. 이 때 만들어진 새로운 특성은 데이터를 더욱 잘 나타내는 특성이 되며, 추출되어 나온 특성의 개수는 당연히 원래 특성의 개수보다 적습니다.
아래는 특성 선택과 특성 추출을 비교하여 나타낸 이미지입니다. 기존 데이터의 특성 $X_m (m = 1,\cdots,n)$ 에 대하여 특성 선택에서는 특성의 개수를 $n$보다 줄이는 방법을, 특성 추출에서는 기존 특성을 조합하여 새로운 특성 집합인 $Z$를 만드는 것을 볼 수 있습니다.

이미지 출처 : github.com/pilsung-kang/Business-Analytics-IME654
아래는 차원 축소를 특성 선택과 특성 추출로 분류한 뒤 방법에 따라 한 번더 분류한 그림입니다.

이미지 출처 : github.com/pilsung-kang/Business-Analytics-IME654
우선 특성 선택 중 필터 방법은 알고리즘을 사용하지 않는 방법이며 정보 획득량(Information gain, IG)이나 오즈비(Odds ratio) 등의 수치를 사용하여 특성을 평가합니다. 래퍼 방법에서는 알고리즘을 사용합니다. 전진 선택법(Forward selection), 후진 제거법(Backward elimination), 유전 알고리즘(Genetic algorithm) 등이 이에 속합니다.
특성 추출은 어떤 것에 중점을 두느냐에 따라 세 가지로 나누어 볼 수 있습니다. 첫 번째는 분산을 최대한으로 보존하는 방법이며 주성분분석(Principle component analysis)이 이 방법에 속합니다. 두 번째는 인스턴스간의 거리 정보를 최대화하는 것으로 다차원 스케일링(Multidimensional scaling)이 있습니다. 마지막으로 잠재된 비선형 구조를 찾는 방법이 있습니다. 지역적 선형 임베딩(Locally linear embedding, LLE), ISOMAP, t-SNE 등이 모두 이에 속합니다.

Comments